3.1 Synchrotron Radiation and Beamline Facilities

The resonant reflectivity measurements for this thesis work were conducted at beamline X6B, National Synchrotron Light Source (NSLS) at Brookhaven National Laboratory.

When electrons are accelerated they lose energy by emission of electromagnetic radiation. In a synchrotron or storage ring the electrons are magnetically constrained to travel round a closed path and the consequent centripetal acceleration results in the emission of the so-called synchrotron radiation. This radiation, once the unwanted by-product of high-energy physics researches, is now a highly developed probe of matter at photon energies from a few electron volts to higher energies (100 keV and more).

The continuum x-radiation provided by synchrotron is up to five orders of magnitude more intensive than conventional sources such as x-ray tubes. This intense synchrotron radiation continuum make it possible for a research worker to select the wavelengths most appropriate for the experiment (i.e. resonant reflectivity measurement) and also to scan the wavelength over a large range, as needed for EXAFS experiments. The synchrotron radiation spectrum can be characterized in terms of a critical energy, which is usually defined as:

(3.1)

The synchrotron x-ray beam is highly collimated. For nonrelativistic energies the radiation emitted by an accelerated electron gives a dipole pattern. For relativistic velocities the dipole pattern is compressed along the direction of motion. Let j be the angle between the observation direction and the electron velocity v in the rest frame and j' in the laboratory frame, the transformation of angle is
 
 

(3.2)

At q = 90° , tanq' »q ' » 1/g . Thus the radiation is emitted in a narrow cone about the tangential direction with a half angular spread of approximately 1/g radians, (cf. Fig. 3.2) or roughly 0.25 mrad (0.014° ) for NSLS. The photon flux given in Fig. 3.1 is integrated over the whole of the vertical distribution. In the plane of the orbiting electrons the observed angular distribution is independent of wavelength due to the time-averaging effect of motion.49

Fig. 3.2 shows the two polarization components, the E vector parallel and perpendicular to the orbital plane. Because the electron is confined to a single orbital plane the radiation is strongly polarized, and is, as shown in Fig. 3.2, close to 100% polarized in the orbital plane. For reflectivity measurements, generally a narrow beam-defining slit is set at the center of the beam, thus the incident x-ray is considered to be 100% s -polarization. As the observation angle moves out of the orbital plane the radiation becomes elliptically polarized. When integrated over all angles and energies the parallel component is found to have seven times the power of the perpendicular component.

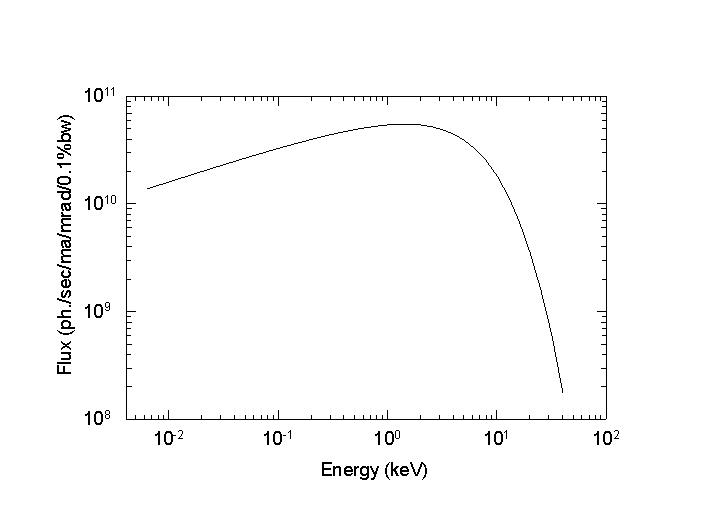
Fig. 3.1 Spectral distribution of synchrotron radiation from NSLS.

Fig. 3.2 Vertical angular distribution of parallel and perpendicular polarization components.
 
 
 
 
 
 

In summary, synchrotron radiation provides an intense, highly collimated and highly polarized continuous spectrum of x-rays for materials studies. However, more laboratory facilities are needed for utilizing the radiation in different experiments, such as monochromator , x-ray mirror and other beamline components.

The X6B beamline has been constructed at a bending magnet port at the NSLS and became a versatile facility for a variety of x-ray experiments. Main components of the X6B beamline include a pair of premonochromator beam slits, a double-crystal fixed-exit monochromator, a double focusing mirror, and a diffractometer, positioned 8.8, 9.8, 12, 24 m away from the source, respectively. Fig. 3.3 shows schematically the arrangement of beamline components.
 
 

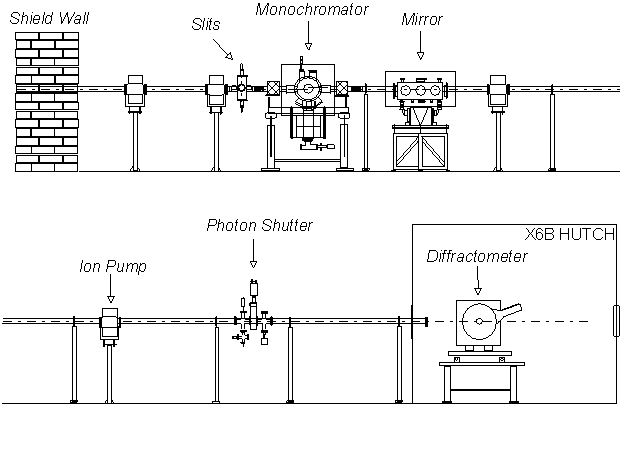
Fig. 3.3 Schematic representation of X6B beamline components.

All beamline components outside the experimental hutch are connected by stainless steel beam pipes, which are maintained in a vacuum of low 10-8 to high 10-9 Torr. The vacuum pass is separated and end-closed by two Be windows. The vertical and horizontal beam slits, upstream the monochromator, were used to control the beam size and energy resolution. The slits are water cooled to dissipate the heat load from the white beam.

In the case of hard x-rays the monochromator design usually takes advantage of the Bragg diffraction planes from single crystals like silicon and germanium. At X6B Si(111) planes are used for energies ranging from 2.34-22.3 keV and Si(220) planes are used for the 3.82-36.0 keV energy range. The energy range is primarily determined by the angle of incidence which varies usually from 57.5° to 5.1° . To make the exit beam travel in the same direction as the incident beam, two pieces of identical single crystals are used for the monochromator. The first crystal acts as a monochromator while the second acts as a reflector. The monochromator is controlled by a single stepping motor with step resolution of 0.09 arcsec, and has a fixed offset of 1 inch between the incident white beam and the exit monochromatic beam. A piezoelectric transducer is used to scan the second crystal with respect to the first crystal. The heat load on the first Si crystal is dissipated through a water-cooled copper block. With Si(111) crystals and a 0.3 mm vertical slits (a vertical acceptance of 0.035 mrad), the energy resolution is 1.4x10-4 at 8.0 keV.

The second optical element is a cylindrical Rh-coated fuse-silica mirror that is bent to a toroid to focus x-rays both vertically and horizontally. The mirror has a fixed sagittal radius of 8.0 cm and an adjustable meridional radius, nominally set to 2500 m for an incidence angle of 6.6 mrad. The 60-cm-long mirror subtends approximately 4.5 mrad horizontally and 0.33 mrad vertically with open premonochromator slits. The root-mean-square roughness of the mirror surface was measured to be 3-5 Å before and after coating with a Rh layer of 800 Å thickness. For a 6.6 mrad angle of incidence, the beam spot at the focal point has a diameter of 0.65 mm (FWHM). The intensity of 8 keV x-rays per mm2 is about 1012 photon/s, three orders of magnitude higher than that of an unfocused beam.52 The mirror also act as a filter to eject the high harmonic components of the monochromatized beam.

The hutch enclosing the experiments has personnel interlock to allow access to the equipment and samples and yet prevent exposure to the synchrotron radiation. The photon shutter prevents the x-ray beam from entering the experimental hutch unless the hutch is locked. For reflectivity and grazing angle EXAFS experiments, the sample is mounted on a high precision goniometer attached to a dedicated six-circle Huber 5020 diffractometer. The goniometer can be manually adjusted or motor controlled to translate the sample relative to the center of the diffractometer. The diffractometer is placed on a kinematic table which can be used to translate and rotate the diffractometer relative to the x-ray beam. The Huber diffractometer allows the sample rotating about axis vertical to the diffraction plane (q scan), inside the diffraction plane (c scan) and normal to the sample surface (j scan). The detector arm (at an angle 2q to the direct beam) can be moved independently or coupled to the sample movement (q -2q scan). The angular movement is controlled by microstep motors with 0.0005° /step precision. A DOS based data acquisition software, EXASCAN, is used to control the monochromator and the diffractometer through CAMAC interface. The system can also be operated with the SPEC/CPLOT, a commercially available software under UNIX.

Three types of x-ray detectors are used for reflectivity and fluorescence EXAFS experiment. They are ionization chamber, NaI scintillation counter and semiconductor detector. Ionization chambers are the oldest and most widely used. These detectors rely on the ability of gas (N2, Ar) to produce ion pairs in response to the ionization radiation. Then, positive and negative ions can be separated in a electrostatic field and form the signal current through electrodes. The detection efficiency of an ion chamber is determined by the active volume, the gas pressure and gas mixing. The ion chambers have the best performance when the signal rate is 105 to 1010 per second. For signal rates below 5´ 104 , the amplifier noise dominates, and pulse counting techniques are therefore preferred. Ion chamber has no energy resolution. In x-ray reflectivity experiments, ion chambers are often used as beam monitors.

The scintillation counters and semiconductor detectors are based on pulse counting techniques. Detectors for which the fluorescence optical radiation resulting from the x-ray absorption process is detected are called scintillation counters. The most widely used scintillating materials are alkali halide crystals such as sodium iodide. The scintillation layer is attached to the front end of the photomultiplier. The photomultiplier converts the fluorescence radiation to electrons and magnifies signals to a detectable level. NaI scintillation detectors have an energy resolution about 3000 eV at 10 keV, barely enough to resolve the harmonic frequencies from the fundamental of the synchrotron radiation. The scintillation lifetime is 270 ns, which limits the pulse pair resolution to about 700 ns. Therefore, scintillation counters lose their linearity when the signal rate is over 5´ 104 and get saturated for higher rates. Scintillation counters are used as scattering signal detectors due to their high sensitivity and compact size.

The semiconductor detector is the solid state analog of the ionization counter. The charge carriers are now electrons and holes rather than electrons and ions, and the ionization potential is the energy required to produce electron-hole pairs, which is 2.97 eV for germanium and 3.73 for silicon at 78 K. Semiconductor detectors have shorter dead times (typically 10 ns) and better energy resolution (typically 200 eV at 10 keV) than scintillation counters.56 The semiconductor detector must be maintained at low temperature: 78 K for germanium detectors, and is very sensitive to the environmental noises. An intrinsic germanium detector is used to measure the x-ray fluorescence in surface EXAFS experiments.
 
 

3.2 X-ray reflectivity experiment

The experiment setup and procedures discussed in this section are based on our research practices and studies of the experimental methodology. Some similar or somewhat different procedures of doing the reflectivity measurements can be found in the literature.

Experimental setup

Fig.3.4 shows the optical setup for x-ray reflectivity measurements. The monochromatized and focused x-ray beam entering the experimental hutch is first monitored by an ion chamber. The ion chamber count (Ioo) is an indicator of the fine tuning state of the monochromator. It is also used as the feed back signal in the monochromator stabilizing system. The beam is then defined by a motorized slit (Slit 1) both vertically and horizontally. The incident beam size (horizontal size w and vertical size d) is very important in the reflectivity measurements. We will show later how the beam size and the detector slit aperture are related to the angular resolution. A NaI scintillation detector (NaI det. 1) is placed perpendicularly to the beam to monitor the incident beam intensity. The air scattering signal collected by the NaI det. 1 in this configuration is proportional to the beam intensity. The reduction factor is about 10-6 for 8 keV beam. The beam then hits the sample and is reflected. Slit 2, slit 3 and the NaI det. 2 are mounted on the 2q arm and moved in the reflection plane to the direction of the reflected beam. The purpose of slit 2 is to cut down any scattering not originating in the sample. Slit 3 is placed before NaI det. 2 and is set wide enough to accept all the specularly reflected scattering. To ensure the best resolution possible and accurate alignment, the aperture of slit 3 has to be close to that of slit 1 but a lit bit wider. The actual size of the slit 3 aperture depends on the beam condition (e.g. focused or partially focused) and the sample property (e.g. Thick, thin or multilayer). Usually trial and error procedure is need to achieve the best resolution. The NaI Det. 2 can be placed perpendicularly or parallel to the beam, depending on the intensity of the reflected beam. A typical reflectivity spectrum can be measured with synchrotron x-ray down to ~ 10-8 while the up limit of the NaI detector count rate is 5´ 104. For this reason, a set of calibrated aluminum absorbers is used to reduce the beam intensity reaching the detector. For fluorescence and grazing angle EXAFS measurements, a semiconductor Ge detector can be placed above the sample or side wise. To reduce the intensity lose due to air scattering , vacuum pipes are used to enclose the x-ray beam pass (not shown in the figure). Fig. 3.5 shows the electronic setup for reflectivity and fluorescence EXAFS measurements. The photon signals collected by the two scintillation counters are transferred to the data acquisition program running on the PC through single channel amplifiers. The energy spectrum of the fluorescence yield detected by the Ge detector can be displayed on a multi-channel analyzer and the fluorescence intensity of specific photo emission lines can be selected by setting the energy window of the single channel amplifier.

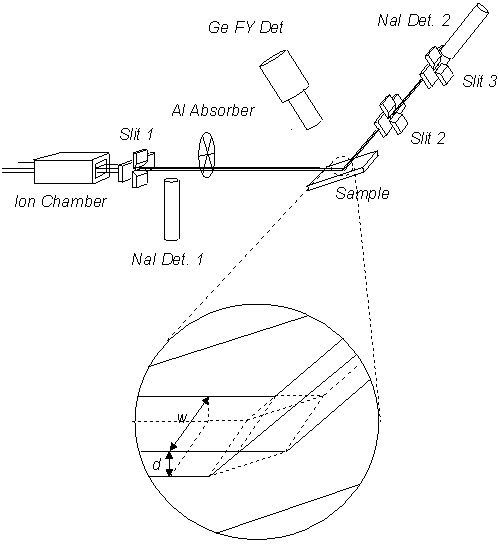
Fig. 3.4 The optical setup for the reflectivity and fluorescence measurements.
 
 
 
 
 
 
 
 
 
 
 
 

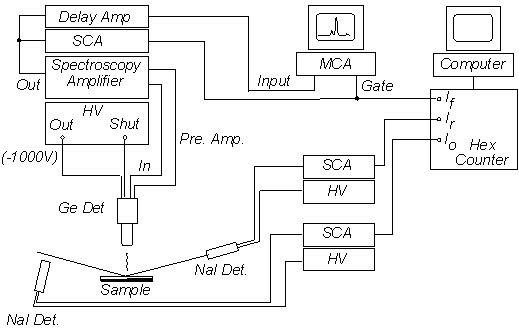
Fig. 3.5 Electronic setup for the reflectivity and fluorescence EXAFS experiments.

The choice of slits

The resolution function of the spectrometer for the reflectivity measurement is defined as the curve obtained by 2q scan of the detector crossing the direct beam. If the beam after slit 1 has an uniformly distributed step function form, the resolution function will assume a shape as shown in Fig.3.6(a). It can be written as:
 
 

(3.3)

(3.4)

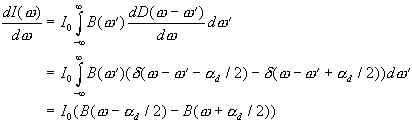(3.5)

(a)

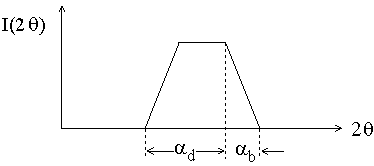
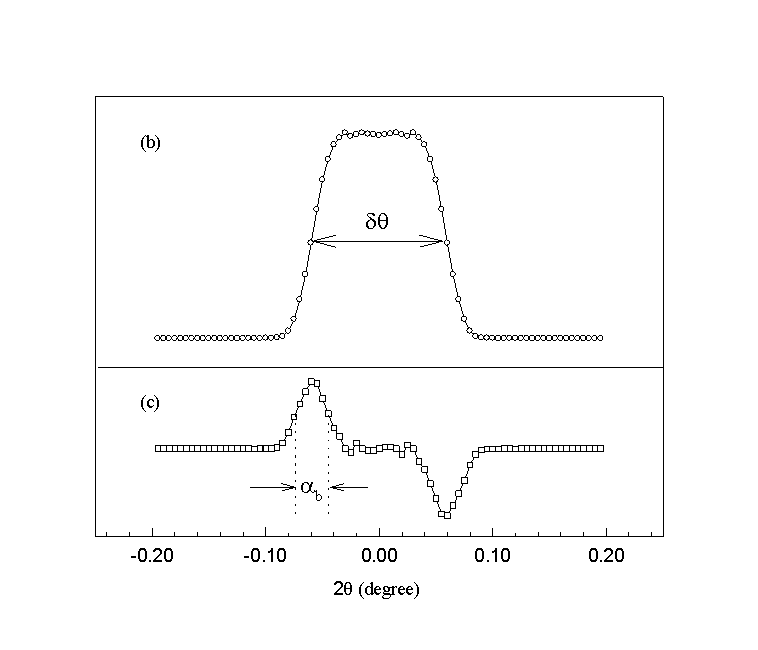
Fig. 3.6 Resolution function of the spectrometer, (a) for step function beam profile, (b) a real case, (c) derivative of (b). The derivative of the resolution function gives the beam profile (cf. Eq. 3.5).

For further discussion, we define the angular acceptance of the detector, dq , as the FWHM of the resolution function. Note that dq depends on both the beam profile and the vertical angular width ad of the detector slit.

It is illuminating to explain the relation between the resolution of the spectrometer and the angular acceptance dq of the detector as well as the angular spread of the incident beam

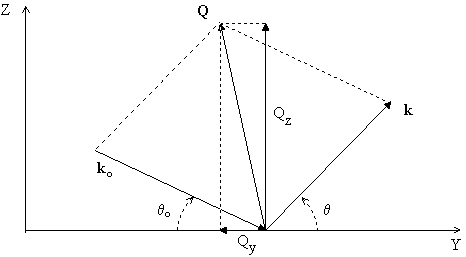
dq0 in terms of the resolution volume in reciprocal space. Fig.3.7(a) defines the momentum transfer Q. It's components in the Y-Z plane (the scattering plane) can be written as:

(3.6)

The uncertainties in Qz and Qy are given by:

(3.8)

(3.9)

(a)
 
 

(b)

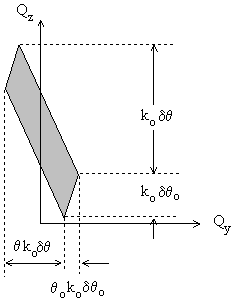
Fig.3.7 Scattering kinematics of reflectivity experiments. (a) Definition of scattering vectors, (b) resulution volume in reciprocal space.
 
 

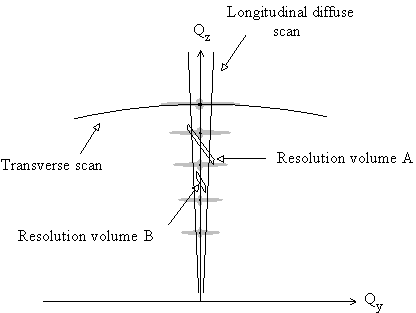
Fig. 3.8 Schematic representation of different resolution volumes in the reciprocal space. Resolution volume A will collect too much diffuse scattering in a specular q -2q scan (along Qz axis). Resolution volume B is adequate for this intensity pattern. Also shown in this figure are the representations of transverse diffuse scan (q scan with the detector fixed at a certain angle (2q ) and the longitudinal diffused scan ( q -2q scan with a fixed offset ). The longitudinal diffused scan gives the background diffuse scattering contribution.

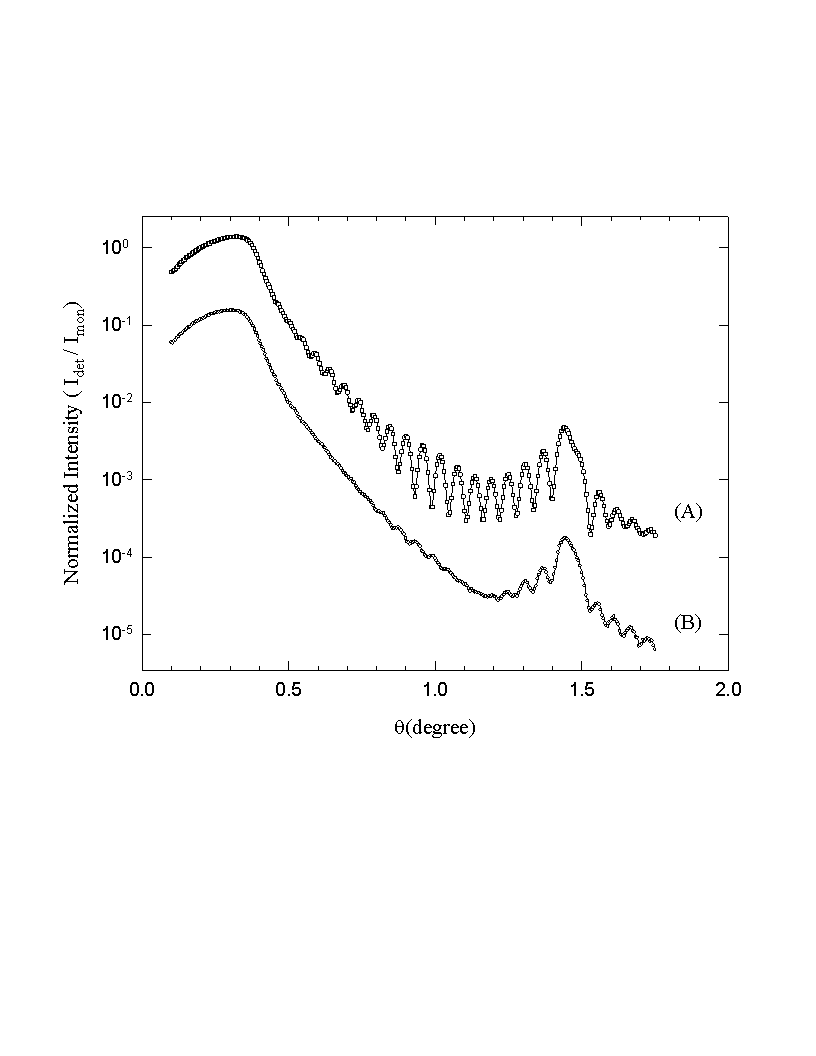
Fig. 3.9 Reflectivity curves measured with different resolution functions. (A) ad = 0.03° , ab= 0.02° , (B) ad = 0.1° , ab= 0.02° . Idet represents the detector counts and Imon the monitor counts. Note that these are raw data curves without geometrical correction.
 
 

In principle, the smaller the resolution volume the better the angular resolution. The vertical width of the beam defining slit (d1) is the most critical parameter since it controls both dq0 and dq(remember d3 must be greater than d1). However, a too small d1 will cause difficulties in sample alignment and reduce the incident beam intensity. In our experiments, we found that a 0.1 to 0.3 mm beam defining slit is adequate for most samples. The detector slit is set accordingly to have ad about twice of ab. This will result in an angular acceptance (dq ) of about 0.1° (cf. Fig.3.6(b)). The horizontal opening of the beam defining slit is usually set to 1 to 5 mm, according to the sample and beam conditions.

Sample Alignment

After correctly setting of the slits, the next step is to align the sample. The object of sample alignment is to align the center of the 2q arm rotation, the sample surface and the beam center to one point. The alignment between the 2q arm center and the beam center is accomplished by translating the diffractometer table in the two directions perpendicular to the beam. Then with both the beam monitor (Imon) and scattering detector (Idet) perpendicular to the beam, a 2q scan crossing the direct beam can be done. The data collected from this scan, Idet/Imon vs. 2q angles, is the resolution function of the normalized beam (cf. fig.3.6). In the following text, by the beam intensity or scattered intensity, we always refer to the normalized intensity as:

(3.10)

With the detector sitting at zero point of 2q , the sample is then translated into the beam by adjusting the goniometer until half of the direct beam intensity is blocked. The parallelism of the sample surface with the direct beam is ensured by rotating the sample about q scan axis. This scan, named as zero point q scan, will result in a curve with triangular line shape. The apex of the triangle is then designated as zero point of q . If the maximum value of the scan is not half of the direct beam intensity, the goniometer has to be adjusted again to raise or lower the sample until half-intensity blocking is reached. Fig. 3.10 shows an example of the zero point q scan curve. The triangle line shape should be symmetric about the zero point of q . A non symmetric triangle means that the beam does not hit on the center of the sample in the direction parallel to the beam. In this case the goniometer has to be adjusted to translate the sample in the beam direction, and above procedure must be repeated to ensure best q alignment. The final zero point q scan curve will be used in determination of the geometrical factor for correction on small angle reflectivity data. We will discuss this point later.

Once this procedure has been carefully followed, the sample is in principle ready for reflectivity measurements. However, it is worth checking the alignment by q scan with higher 2q angles, for example at the critical angle of total reflection or/and Bragg peaks of multilayers. Any missetting of the sample is then easily discovered if the sharp specular peak does not sit at the q angle of exactly half of the fixed 2q angle (cf. fig. 3.13). Usually the missetting , if any, is very small (e.g. 0.005° ) and can be corrected by recalibrating the q angle.

Data collection, correction and analysis

The specular reflectivity is measured by q -2q coupled scans. In a q-2q scan the detector and the sample rotate simultaneously and the moving step of the detector is kept to be twice of the sample. Since the incident angle q0 and scattering angle qare equal, the Qy in (3.6) is zero and the scan viewed in Q-space is along the Qz axis. To avoid saturation of the detector, different aluminum absorbers are inserted in the beam to attenuate the intensity at different angular regions. A completed continuous reflectivity curve can be obtained by connecting the segments of the curve measured with different absorbers. The shifting constants needed for doing this can be obtained from the overlapped parts of the segments. The absolute reflectivity is obtained, if all the beam is intercepted by the sample, by dividing by the direct beam intensity.

For small angles, the beam is not fully intercepted by the sample (cf. Fig. 3.11). In this case, only part of the incident beam hits on the sample and a geometrical correction is needed to get the absolute reflectivity. The part of the beam intensity intercepted by the sample, I0'(q0) can be derived from the zero point q -scan function Iz(q0) :

(3.11)

(3.12)

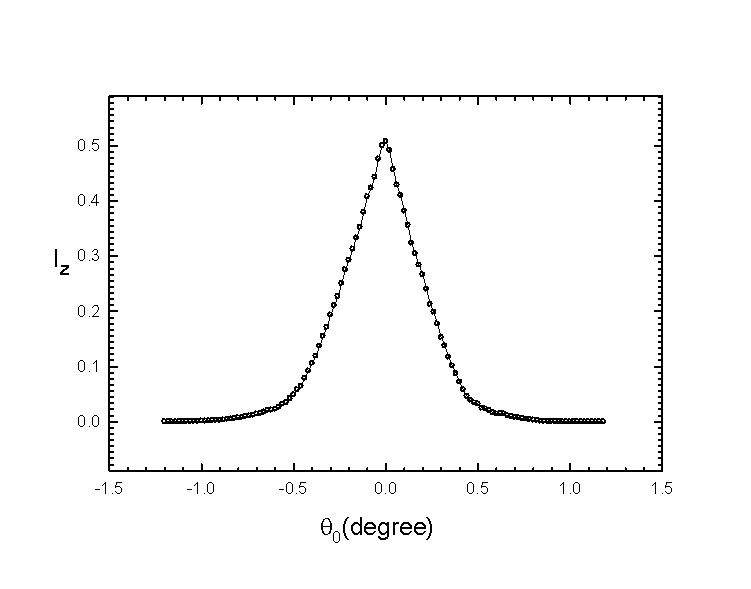
Fig. 3.10 An example of the zero point q -scan curve. Iz is normalized intensity.
 
 

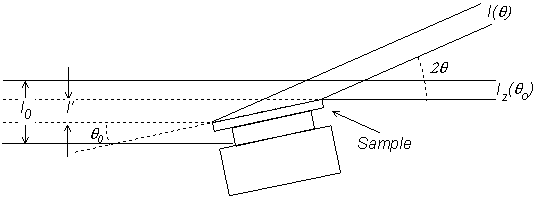
Fig. 3.11 Diagram of the beam split for incident angles less than the full interception angle.

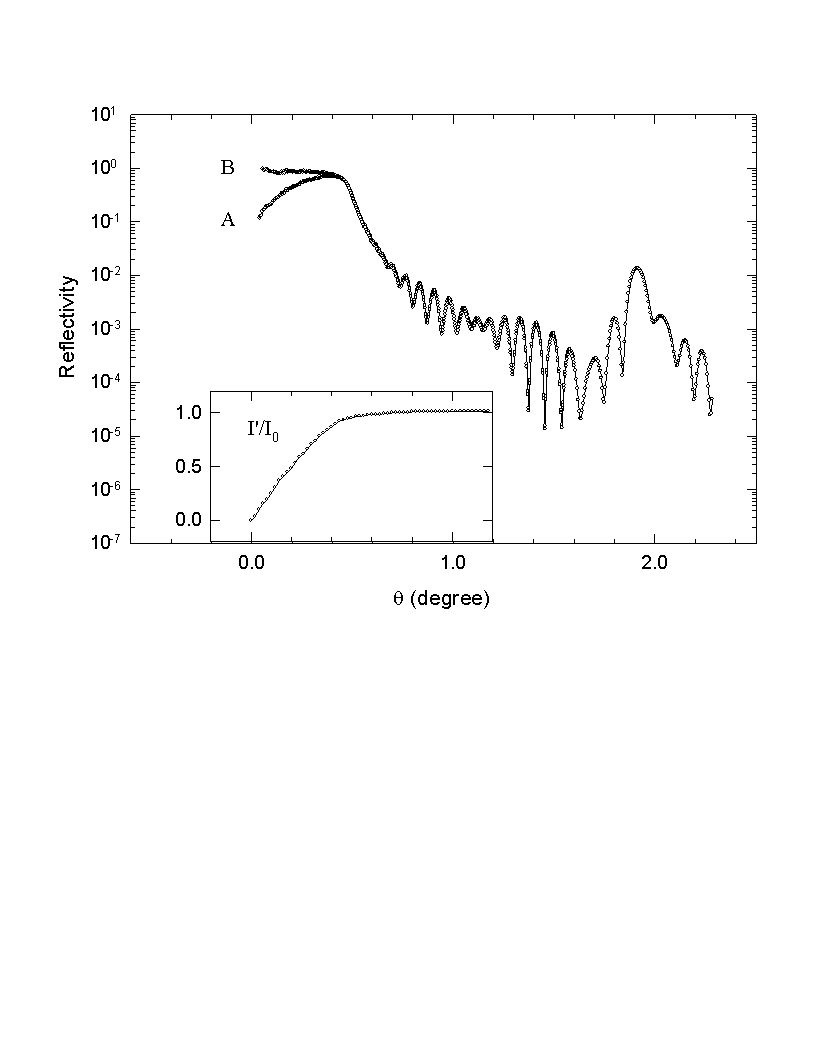
Fig. 3.12 The geometrical correction for small angle data. Curve A is the data before the correction, B the data after the correction. The insert shows the ratio between the intercepted intensity I' and the direct beam intensity I0.

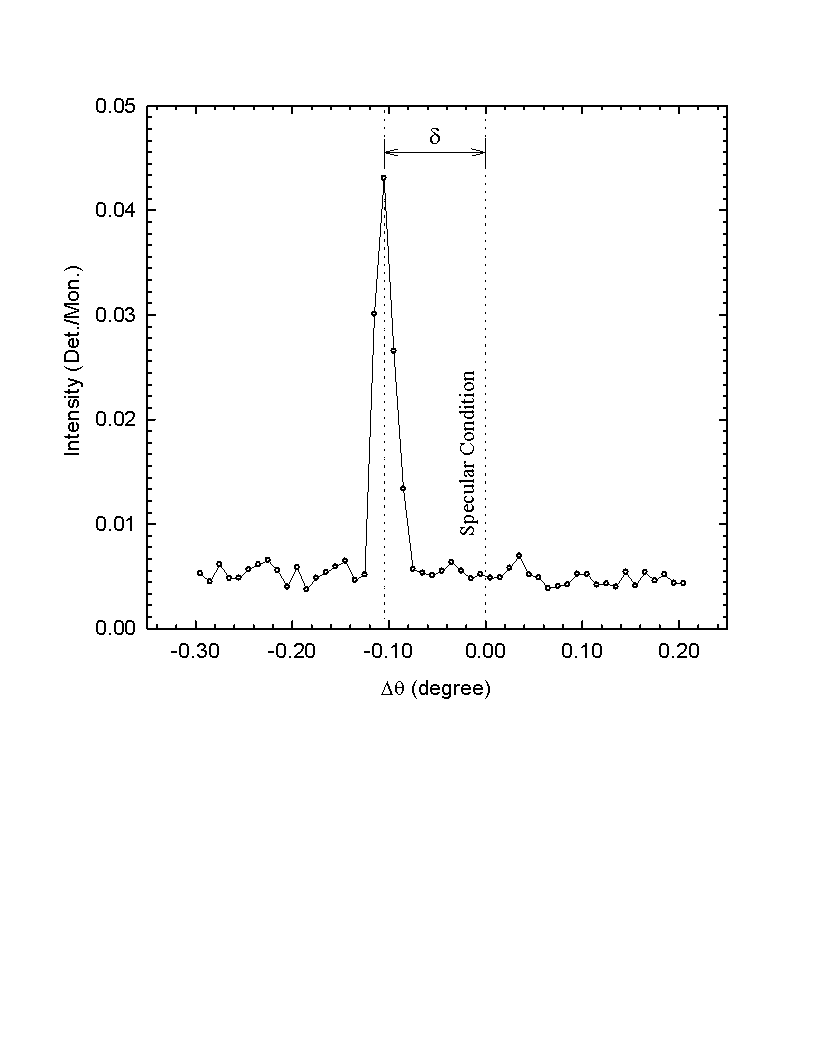
Fig. 3.13 A transverse scan with 2q fixed at 10.39° . Dq is relative to the specular condition. In this scan the sample is offset to the specular condition by an d about 0.1° .

Another applicable correction is the subtraction of the diffuse background scattering from the raw data curves. Because of the finite resolution of the spectrometer, part of the diffuse scattering background may be included into the detected specular intensity. When the diffuse scattering contribution is comparable to the specular component, it has to be subtracted from the raw data to get the true specular reflectivity. For doing this, two kinds of scan related to diffuse scattering are needed: the transverse scan and the longitudinal diffuse scan. Fig.3.8 shows the loci of these scans in Q-space. Transverse scans are carried out by rotating the sample (q -scan) while keeping the detector fixed at a certain angle (2q ). The intensity curve from a transverse scan is composed of a sharp specular peak and a slow varying diffuse scattering background. The amount of diffuse scattering to be subtracted is determined by the longitudinal diffuse scans. In a longitudinal diffuse scan the sample is offset from the specular condition by a small and fixed angle d . The offset d can be set to both sides of the specular peak (see fig. 3.13). To get the best estimate of the diffuse scattering contribution, the offset angle should be as small as possible but without collecting any specular intensity. The true specular reflectivity is then given by:

(3.13)

Where  is the longitudinal diffuse scattering intensity collected with an offset d from the specular ridge. The diffuse scattering level relative to the specular peak is a test of the adequacy of the spectrometer resolution. If the diffuse scattering level is too high, one should first try resetting the slits to reduce the resolution volume. For the reflectivity data used in this thesis, the diffuse scattering level is at most less than 10% of the total intensity. Fig. 3.14 shows an example of diffuse scattering correction.

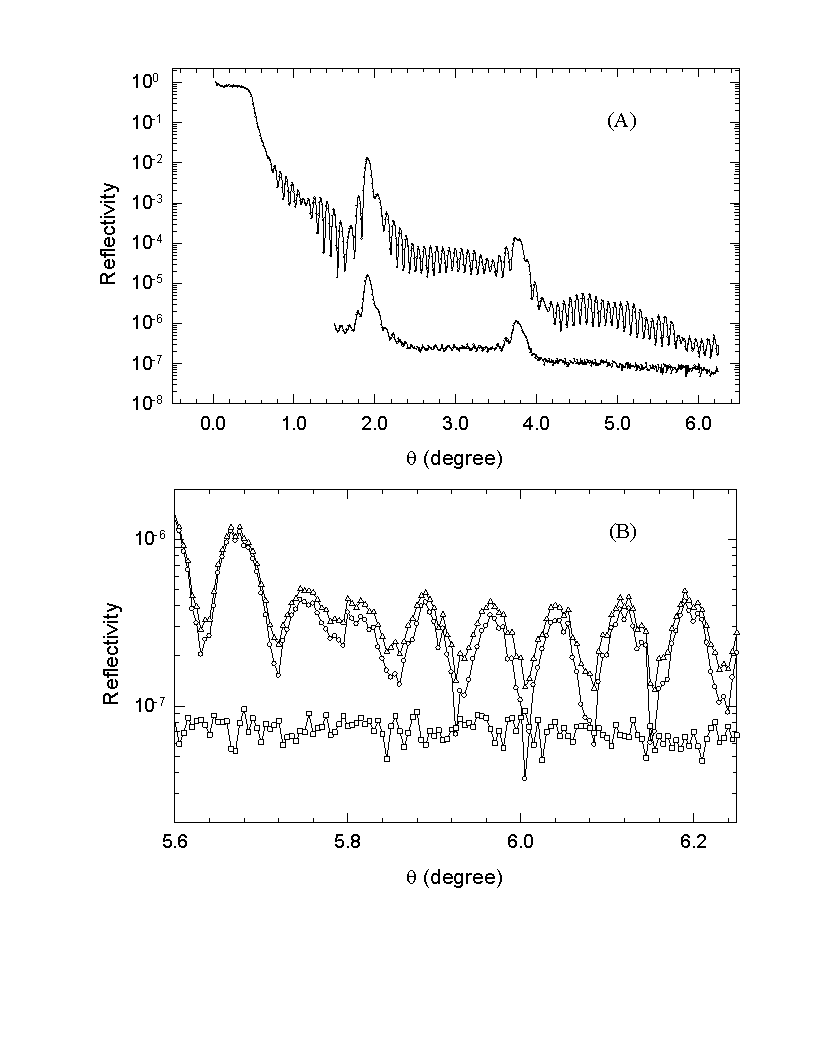
Fig. 3.14 Diffuse scattering subtraction. (A) shows the diffuse scattering level in comparison to the reflectivity data before correction. The offset for the diffuse scattering scan is 0.1° . (B) shows in details the reflectivity data before correction (triangles), after correction (circles) and the diffuse scattering intensity (squares). The data is taken from a Cr/Fe multilayer with an x-ray beam of 6.1 keV.

The object of the reflectivity measurement is to derive the structural parameters from the measured reflectivity curves. Reflectivity data analysis is actually a process of nonlinear least-squares curve-fitting of the model calculation to the experimental data. That is, to find out the parameters that minimize the least-squares sum:

(3.14)